Sobre el Financial Times y la efectividad de los confinamientos
Hay casos de Covid-19 en todo el mundo. También hay muertos en todo el mundo. Desde que empezó la pandemia vemos todos los días un diluvio de cifras y datos sobre la situación sanitaria aquí y allá, y yo personalmente no sé por qué en unos sitios hay más muertos que en otros. Por supuesto tengo teorías, igual que cualquiera que se haya parado a pensar en ello. Pero las teorías no encajan muy bien con la enorme variedad de situaciones entre países o incluso dentro de un mismo país.
Pongamos Japón como ejemplo. El país tiene la población más envejecida del mundo, sólo hace test a quien muestre síntomas de la enfermedad, no hace rastreo de contactos y no ha confinado a la población. Por si fuera poco, los japoneses usan los trenes y metros más que nadie. A pesar de hacerlo aparentemente todo mal (o más bien no hacer nada) y tener las condiciones ideales para una hecatombe sanitaria, desde Enero hasta el 10 de Mayo sólo han muerto por coronavirus unos 600 japoneses.
Tal vez el gobierno de allí esté disimulando las cifras. Pero si hubiese diez muertos más que lo que dicen las fuentes oficiales seguiríamos preguntándonos cómo pueden ser tan pocos.
Algunos investigadores creen que el haber sido infectado previamente por los otros coronavirus, responsables de parte de los resfriados, podría otorgar inmunidad frente al Sars-CoV-2. Esa exposición a los otros coronavirus no tiene por qué ser homogénea alrededor del mundo, así que parte de la variación en la mortalidad del Covid-19 podría deberse simplemente a que unas poblaciones tienen más inmunidad que otras. Y tal vez las diferencias genéticas entre poblaciones causen también diferencias en mortalidad. Simplemente no lo sabemos, así que es muy precipitado decir que un país ha gestionado la pandemia “mejor” que otro por el mero hecho de haber sufrido menos muertos.
Centrándonos en las cosas que podemos decidir, la mayor controversia en el Covid-19 se refiere a la efectividad de los confinamientos. Como hay unas doscientas naciones y las posibilidades para comparar unas con otras son infinitas, decir que un confinamiento es útil (o inútil) en base a la comparación de sólo dos países no tiene sentido. Uno podría argumentar que el confinamiento de Noruega es el motivo por el que esa nación ha tenido menos muertos que Suecia, pero la conclusión contraria se obtendría si comparásemos Bélgica con Países Bajos. Un argumento serio tiene que mirar a una muestra representativa de países, o de regiones con datos de mortalidad más o menos fiables. Por supuesto seguirá habiendo muchos otros factores aparte del confinamiento que influyan en la mortalidad, pero al elegir una mayor cantidad y variedad de países esos otros factores tendrán menos importancia.
Tengo una mala opinión de los confinamientos, y a lo mejor por eso me entero principalmente de los argumentos y datos en contra, y no de los que hay a favor. Aún así, me llama la atención la ausencia de gráficas o tablas que hagan ese tipo de comparativa sistemática y encuentren un efecto positivo del confinamiento. La única que recuerdo es esta, del Financial Times. Fue publicada el 14 de Abril y apareció también el 1 de Mayo en un artículo de The Conversation defendiendo los confinamientos. El FT argumenta de forma explícita en el título: cuanto más tarde se decretó un confinamiento, más muertos acabó teniendo ese país.
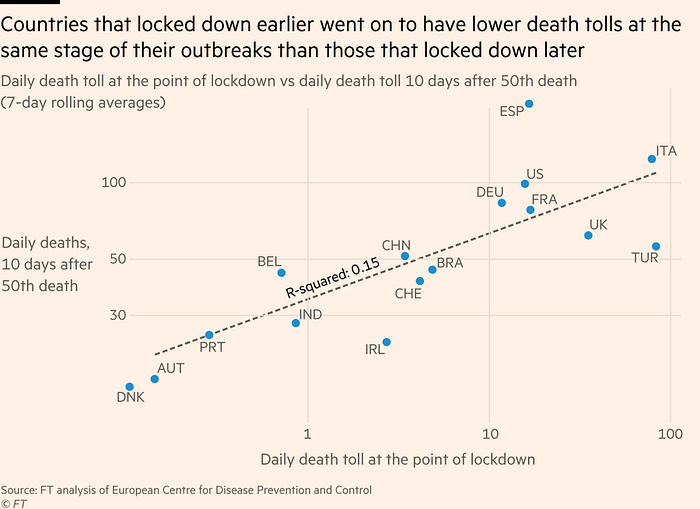
(Usando una escala logarítmica los ejes no pueden empezar en 0)
Vamos a desgranarla un poco. En primer lugar, la selección de países parece rara, pero el FT lo defiende porque dice que siempre ponen la misma selección, para ser consistentes (o al menos tenían esa selección cuando la publicaron). No voy a discutir si los datos de mortalidad para cada nación son correctos — asumo que lo son.
En el eje horizontal tenemos los fallecimientos que había en el momento de imponer el confinamiento; podría decirse que representa la tardanza del confinamiento. El FT usa una media de 7 días para evitar irregularidades, porque podría dar la casualidad de que justo el día que se decretó el confinamiento las muertes fuesen muchas o muy pocas. Hasta aquí todo bien.
En este tipo de gráficas se suele decir que el eje horizontal representa la variable independiente, la “causa”, mientras que el vertical representa la variable dependiente o “efecto”. Entre comillas porque, precisamente, lo difícil es demostrar una relación causa-efecto. Así, la decisión de imponer el confinamiento en un momento u otro (cuando un país sufría más o menos muertos al día) se toma como causa en esta gráfica.
En el eje vertical está el problema. El FT ha escogido, para medir el efecto de esa decisión de confinamiento, los fallecimientos diarios que tenían lugar 10 días después de la 50ª defunción. Si te parece rebuscado no eres el único. Por un lado tiene sentido que se midan los fallecimientos a partir de cierto mínimo, porque así excluyes a países muy pequeños o que eliminaron la enfermedad muy rápido (Islandia, Taiwan, etc). Es decir, con ese límite uno se asegura estar analizando países con un brote serio. Pero, por otro lado, un país puede pasar de los 50 fallecimientos sin confinamiento. ¿Entonces qué ocurre con la gráfica?
Además, de media pasan unos 20 días entre contagio y fallecimiento. Si un país decreta el confinamiento cuando ya se han superado los 50 fallecimientos, como ocurrió en muchos casos (España sin ir más lejos), aunque el confinamiento causase una reducción en los contagios sería prácticamente imposible que se reflejase en la gráfica, porque el eje vertical muestra lo que ocurre unos 10 días después de ese 50º fallecimiento. (Técnicamente, muestra la media de los días 7º a 13º tras ese fallecimiento). Tendría más sentido que el eje vertical reflejase los fallecimientos en base a los días transcurridos desde que empezó el confinamiento, no los días transcurridos desde la muerte número X.
A los periodistas/analistas del FT les preguntan muchas veces por qué sus gráficas muestran muertes en cantidades absolutas, y no per cápita. Ellos responden que apenas hay correlación entre la población de un país y la cantidad de muertes. Si esa afirmación te sorprende, tranquilo, porque es falsa; la correlación entre población total y muertes es muy clara si tomas una muestra de países más amplia.
Entonces tenemos una gráfica que muestra una correlación entre la tardanza del confinamiento y la mortalidad. La pregunta es, ¿esta relación es real? ¿O es simplemente resultado de una extraña selección de países y medidas?
Para comprobarlo he querido ver qué ha pasado en los países o territorios que han tenido brotes significativos pero no llegaron a decretar el confinamiento. Excluyo a Japón porque, como expliqué al principio, la evolución del Covid-19 allí es inexplicable y tal vez lo que ocurre en ese país no se pueda extrapolar a ningún otro sitio. Para evitar ambigüedades tampoco incluyo a Países Bajos, que técnicamente no ha tenido “confinamiento” (se ha mantenido la libertad de circulación) pero ha cerrado muchos negocios. Eso nos deja con:
- Suecia
- Varios estados de EEUU. Algunos superan la barrera de los 50 fallecimientos pero no por mucho. Escojo a los dos que no han decretado confinamiento pero han sufrido cientos de muertes: Iowa y Oklahoma.
(La gráfica del FT muestra un sólo punto para EEUU, pero con la variedad de políticas que han aplicado los distintos estados no creo que eso tenga sentido)
Suecia había sufrido un acumulado de 49 defunciones para el 22 de Marzo, y 60 para el día siguiente. 10 días después la media móvil de fallecimientos era 58 (1 de abril) o 65 (2 de abril). Escojo 60 fallecimientos al día como punto intermedio — la cifra exacta no es importante.
En Iowa el fallecimiento número 50 tuvo lugar el 15 de Abril. Para el 25 de Abril, la media diaria era de 8,28 muertes. Con respecto a Oklahoma, superó las 50 muertes acumuladas el 6 de Abril y para el 16 de ese mes la media diaria era de 6,28 fallecimientos.
El FT no publica los datos usados para generar sus gráficas, cosa que respeto ya que bastante esfuerzo cuesta producirlas. Para replicar su gráfica lo que he hecho ha sido, con WebPlotDigitizer, calcular el valor de los dos extremos de la recta de regresión. Entre ambos puntos dibujo una recta que queda con la misma pendiente la misma que la original, o prácticamente la misma.
Luego veo a qué altura en la gráfica estarían Suecia, Iowa y Oklahoma si el FT los hubiese incluido. La posición en el eje horizontal es simplemente la que corresponda a una determinada altura de la recta de regresión. Recuerda que el eje horizontal representa el ritmo de fallecimientos que ocurría cuando se declaró el confinamiento. Estos tres territorios no llegaron a confinarse, así que la posición de los puntos a lo largo del eje horizontal es simbólica.

Sorpresa: Iowa y Oklahoma nisiquiera llegan a la línea. El punto más bajo de la recta está en algo más de 20 defunciones al día, y estos dos estados por suerte se han quedado muy lejos. Interpretada de forma literal, la regresión del FT significaría que incluso un país o territorio que declarase el confinamiento cuando aún tenía 0 muertos diarios acabaría sufriendo 20 muertes al día. Pero no ocurrió.
Alguno dirá que la relación entre tardanza del confinamiento y cantidad de muertes se rompe en poblaciones muy pequeñas. Yo contesto que la población de Iowa y Oklahoma es comparable a la de Irlanda y Dinamarca, dos países que sí aparecían en la gráfica del FT (aunque Dinamarca también quedaba por debajo del límite inferior de la recta).
Pero el caso más interesante es el de Suecia. Allí los fallecimientos diarios representados en el eje vertical (60) corresponden a los que “debería” tener un país que decretó el confinamiento con 8 fallecimientos al día (eje horizontal). Sin embargo Suecia nunca lo declaró: ni con 8 muertos al día ni con 80. En todo momento se han mantenido abiertos los hoteles, restaurantes, colegios, etc.
Así que diría que la gráfica del FT no demuestra nada respecto a la efectividad de los confinamientos.
Datos y código
Los datos para Iowa están aquí. Aunque los fallecimientos se anuncian a diario, no hay (o al menos no he encontrado) una lista con el acumulado. Para eso he usado la página de Wikipedia.
Respecto a Oklahoma, la página oficial es más intuitiva, y muestra una gráfica con el acumulado de fallecimientos día a día.
Esta es la web oficial con datos sobre el Covid-19 para Suecia, y aquí hay un CSV con las cifras.
Por último, el código para la gráfica de este artículo está aquí.